by Israr Ahmed
In this Article we look at the academic definition of how Black Scholes is used to value options on forwards/futures – in the context of delayed payment from exercise date. We then look at how this is implemented in Endur. We also have a version of the Endur BS Formula in an online Spreadsheet format.
Academic Model
Black 76
Black Scholes is used to price Spot prices. To model Future/Forward prices we assumes Futures are like a stock paying dividend q equal to r. The standard Black-Scholes with dividend collapses into:
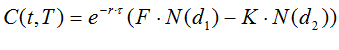
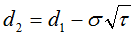
Black 76 extension: Delayed Payment Date
In reality the actual Payment Date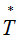 
generally occurs later than the Expiry Date 
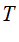ie 
.
We can think of the derivative becoming a cash position (equal to it’s value) at expiration. Such a cash position does not accrue interest until payment date. Therefore this type of contract must be further discounted to take into account the delay in payment.
= 
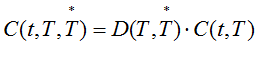
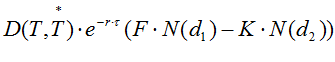(A)
where 
is the discount from the Payment Date back to the Exercise Date ie
now substituting this into (A) we can also re-write
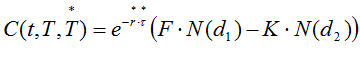(B)
(A) and (B) are equivalent
where
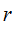is the zero rate at Expiry Date 
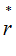is the zero rate at Payment Date 
OpenLink Model
OpenLinks B-S ( Black 76 ) Model with Delayed Payment Date
There are a number of modifications to consider:
- OpenLink sets q (the dividend) to = r (risk free rate) so that the B-S Model essentially becomes the Black 76 Model
- OpenLink actually calculates the B-S (ie Black 76) value as at the Payment Date using the modified Black 76 extension shown above.
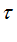= time to Expiration (with CC Zero Rate r )
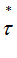= time to Payment (with CC Zero Rate 
)
Given that
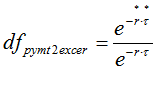
then 
The formula can then be written in two different way – essentially exactly the same – but Formula 2 is more explicit.
Formula 1 ( as implemented by OpenLink )
Formula 2 (more explicit)
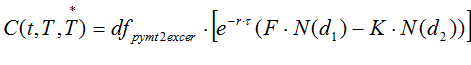
where we have the usual , time t (exercise date ) calculated;
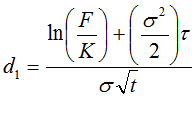
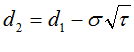
Note: OpenLink gets the value for  {ie ‘R’ in model input screen} by recalculating the CC Zero Rate using Act/365 rather than what is on the LIBOR curve setting |