By Israr Ahmed
VaR is a measure of the expected loss over a given time horizon at a given confidence interval (under normal market conditions).
| For example, if a portfolio of stocks has a one-day 5% VaR of $1 million, there is a 5% probability that the portfolio will fall in value by more than $1 million over a one day period.Informally, a loss of $1 million or more on this portfolio is expected on 1 day out of 20 days. The probability level is more often specified as one minus the probability of a VaR break, so that the VaR in the example above would be called a one-day 95% VaR instead of one-day 5% VaR.
|
Single Asset
Commonly held that returns are log normally distributed. In which case the underlying price follows the following path:
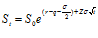
where Z is a random standard normal variable N(0,1) and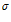 
is the volatility of returns.
Say the graph below represents the probability density function of the log returns of a such a single asset over a t day horizon;
Note that if returns are log normally distributed, then the log of the returns are normally distributed.
(Fig1)
Then VAR at x% confidence interval (where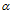 
is the number of standard deviations corresponding to the confidence interval x%) over this t day horizon is
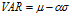
For practical purposes the VAR horizon is assumed to be small (1 to 2 days) and so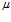 
is assumed to be zero.
Hence
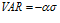[ as indicated by arrow on Fig 1 ]
Furthermore VAR is presented as a positive number so we arrive at :
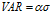
Two Assets
The above is VaR for a single asset. A portfolio is made up of many deals/assets, each with prices returns (log) that have their own volatilities. So for VaR across multiple assets portfolio we need to compute the single Volatility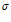 
of this portfolio.
For two assets the following result holds (assuming normal distribution)
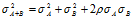
Thus correlations are required in order to calculate multi asset portfolio variance .
From this we obtain ( for 2 assets )
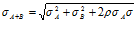
This can then be used in the same above VAR equation
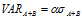
This can be extended to multiple asset portfolios which we shall demonstrate in the next VaR article.
